
Statistiques d’expériences: Bravo ! Vous venez de réaliser votre première expérience dite parapsychologique, vous obtenez de bons résultats a priori. Mais justement, pouvait-on atteindre le même résultat par hasard? Est-ce vraiment exceptionnel de parvenir à trouver par exemple 4 fois de suite le bon résultat entre pile ou face?
Nous vous proposons ici une petite escapade vulgarisée pour comprendre comment calculer des statistiques pertinentes pour vos projets.
Statistiques et probabilités sont intimement liées. Nous allons parcourir un exemple simple que vous pouvez reproduire facilement chez vous : le jeu de pile ou face. Nous ne vous rappellerons pas les règles, mais faisons un tour d’horizon de ses caractéristiques :
- Un lancer est obligatoirement suivi d’un résultat parmi 2 choix possibles.
- Les 2 choix sont uniquement : pile ou face (on exclut la tranche).
On vulgarise le jeu ainsi : à chaque lancer, le joueur a 1 chance sur 2 de trouver le bon résultat. On admet que la pièce n’est pas truquée et qu’elle est tout à fait normale (symétrique, un poids également réparti sur toutes les faces, …). On dit en mathématique que notre système (la pièce de monnaie) est équilibré.
Ceci est très important, car cela signifie qu’on a autant de chance de tomber sur pile que sur face. Ainsi, pour évaluer notre probabilité de réussite, nous pouvons en déduire qu’elle est de 50%, 1 chance sur 2, ou encore p = 0,5.
Admettons que nous souhaitons lancer cette pièce 50 fois de suite et prédire juste avant le résultat. Nous avons 50 fois de suite 1 chance sur 2 de réussir (et autant de se tromper). Mais la vraie question est la suivante : à partir de combien de bonnes prédictions je serai capable de conclure que j’ai réellement prédit l’avenir? Autrement dit : sur mes 50 lancers, combien m’en faut-il de correctement prédits pour conclure que je peux deviner le résultat?
Il existe des protocoles, pour la plupart médicaux sur lesquels nous allons nous appuyer. En effet, pour constater certains phénomènes médicaux, comme l’efficacité des vaccins, on estime que le test est réussi quand on a moins de 1% de chances d’y parvenir par hasard. Personnellement, nous nous sommes fixés le même seuil.
Revenons-en à nos moutons, nous avons :
- un nombre déterminé de lancers – et donc de résultats : n = 50.
- la probabilité de réussir à chaque lancer : p = 0,5.
- un seuil à atteindre pour qualifier notre expérience de réussie : moins de 1%.
Pour calculer notre nombre de lancers minimum pour de telles statistiques, penchons-nous sur les mathématiques et la loi binomiale. Pour l’exploiter, nous utilisons le logiciel en ligne GeoGebra.
Entrons toutes ces données et nous obtenons le graphique suivant :
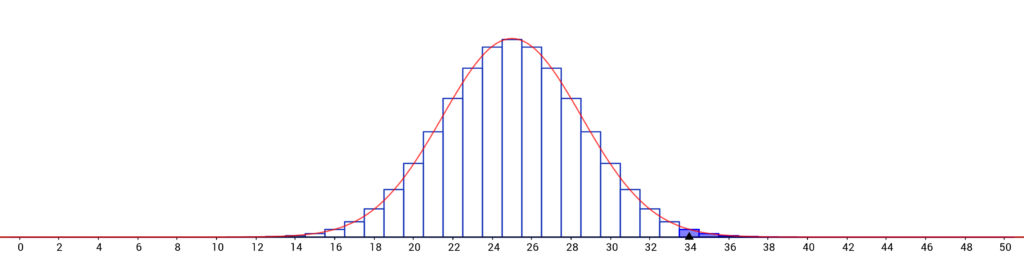
Sur ce graphique, nous pouvons lire la probabilité en fonction du nombre de lancers réussis par hasard. Nous insistons sur le terme « par hasard », car il sera notre base de comparaison. Il apparaît que par hasard, sur 50 lancers, nous avons une grande chance d’obtenir aux alentours de 25 bonnes réponses (en gros 52% de chances d’obtenir un résultat entre 23 et 27 bonnes prédictions).
Qu’en est-il de notre seuil à moins de 1% ? Il ne se trouve pas si éloigné : sur nos 50 lancers, si vous prédisez au moins 34 bons résultats, vous franchissez ce seuil avec un taux de réussite par hasard égal à 0,77%.
À vous de jouer, soit avec cet exercice, soit avec le votre. Dans tous les cas, utilisez :
- La loi binomiale,
- Le nombre d’échantillons ou de résultats, noté n,
- La probabilité de réussite de chaque résultat, notée p.
Bon travail.

